1. Spearman's correlation coefficient, (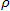 , also signified by rs) measures the strength of association between two ranked variables.
, also signified by rs) measures the strength of association between two ranked variables.
2. Assuming that there is a monotonic relationship between your variables. A monotonic relationship is a relationship that does one of the following:
a) as the value of one variable increases, so does the value of the other variable.
b) as the value of one variable increases, the other variable value decreases.
Examples of monotonic and non-monotonic relationships.
3. A monotonic relationship is an important underlying assumption of the Spearman rank-order correlation. It is also important to recognize the assumption of a monotonic relationship is less restrictive than a linear relationship.
4. How you report a Spearman's correlation coefficient depends on
whether or not you have determined the statistical significance of the
coefficient. If you have simply run the Spearman correlation without any
statistical significance tests, you are able to simple state the value
of the coefficient as shown below:
However, if you have also run statistical significance tests, you need to include some more information as shown below:
where df = N - 2, where N = number of pairwise cases.
5. The general form of a null hypothesis for a Spearman correlation is:
H0: There is no association between the two variables [in the population].
Remember, you are making an inference from your sample to the
population that the sample is supposed to represent. However, as this a
general understanding of an inferential statistical test, it is often not included. A null hypothesis statement for the example used earlier in this guide would be:
H0: There is no association between maths and English marks.
6. It is important to realize that statistical significance does not
indicate the strength of the Spearman rank-order correlation. In fact,
the statistical significance testing of the Spearman correlation does
not provide you with any information about the strength of the relationship. Thus, achieving a value of p = 0.001, for example, does not mean that the relationship is stronger than if you achieved a value of p
= 0.04. This is because the significance test is investigating whether
you can accept or reject the null hypothesis. If you set α = 0.05,
achieving a statistically significant Spearman rank-order correlation
means that you can be sure that there is less than a 5% chance that the
strength of the relationship you found (your rho coefficient) happened
by chance if the null hypothesis were true.
(Adapted from: https://statistics.laerd.com/statistical-guides/spearmans-rank-order-correlation-statistical-guide.php)
*Exercise on Spearman's Rank-order Correlation.
(Adapted from: https://statistics.laerd.com/statistical-guides/spearmans-rank-order-correlation-statistical-guide.php)
*Exercise on Spearman's Rank-order Correlation.



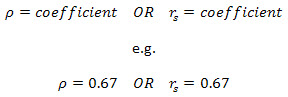
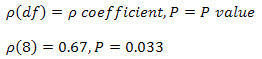
No comments:
Post a Comment